Derivative of Inverse Trigonometric Functions arccot(x) using Implicit Differentiation

Welcome to our comprehensive tutorial on solving derivative of an inverse trigonometric function! If you've ever found yourself struggling with the intricacies of calculus or yearning to unlock the secrets of this mysterious functions, you've come to the right place. In this guide, we will take you on an enlightening journey through the world of inverse trigonometric derivatives, unraveling their complexities and providing with clear and intuitive understanding on how to conquer them.

$$ arccot (x)$$

Let us solve for arccot(x) by equating the problem with y:

$$ y = arccot(x)$$

Isolate x by taking the cotangent of both sides:

$$ {\color{#FF0000} cot}  y =  {\color{#FF0000} cot} (arccot(x))$$

Cancel the arc cotangent using its inverse function cotangent which will result to x, opposite functions in trigonometry undo the effect of each other:

$$cot(y) = \bcancel{cot} (\bcancel{arccot}(x)) $$

 $$ cot(y) = x$$

We can prove this by substituting 1 as x. If we first take the inside function arccos(1), we will have 0. and if we solve cos(0), it will return to the original value of x which is 1. 

Find the derivative of both cot(y) using chain rule and x using power rule:

$$\color{#0000FF}  -csc^2(y) \color{#000000} \cdot \color{#008000} \dfrac{dy}{dx}   \color{#000000} = 1$$

Isolate ^dy/_dx by multiplying both sides by ¹/_-csc²(y):

$$\dfrac{\bcancel{-csc^2(y)}\dfrac{dy}{dx}}{\color{#FF0000} \bcancel{-csc^2(y)}}  =  -\dfrac{1}{\color{#FF0000} csc^2(y)}  $$

$$ \dfrac{dy}{dx} = -\dfrac{1}{csc^2(y)} $$

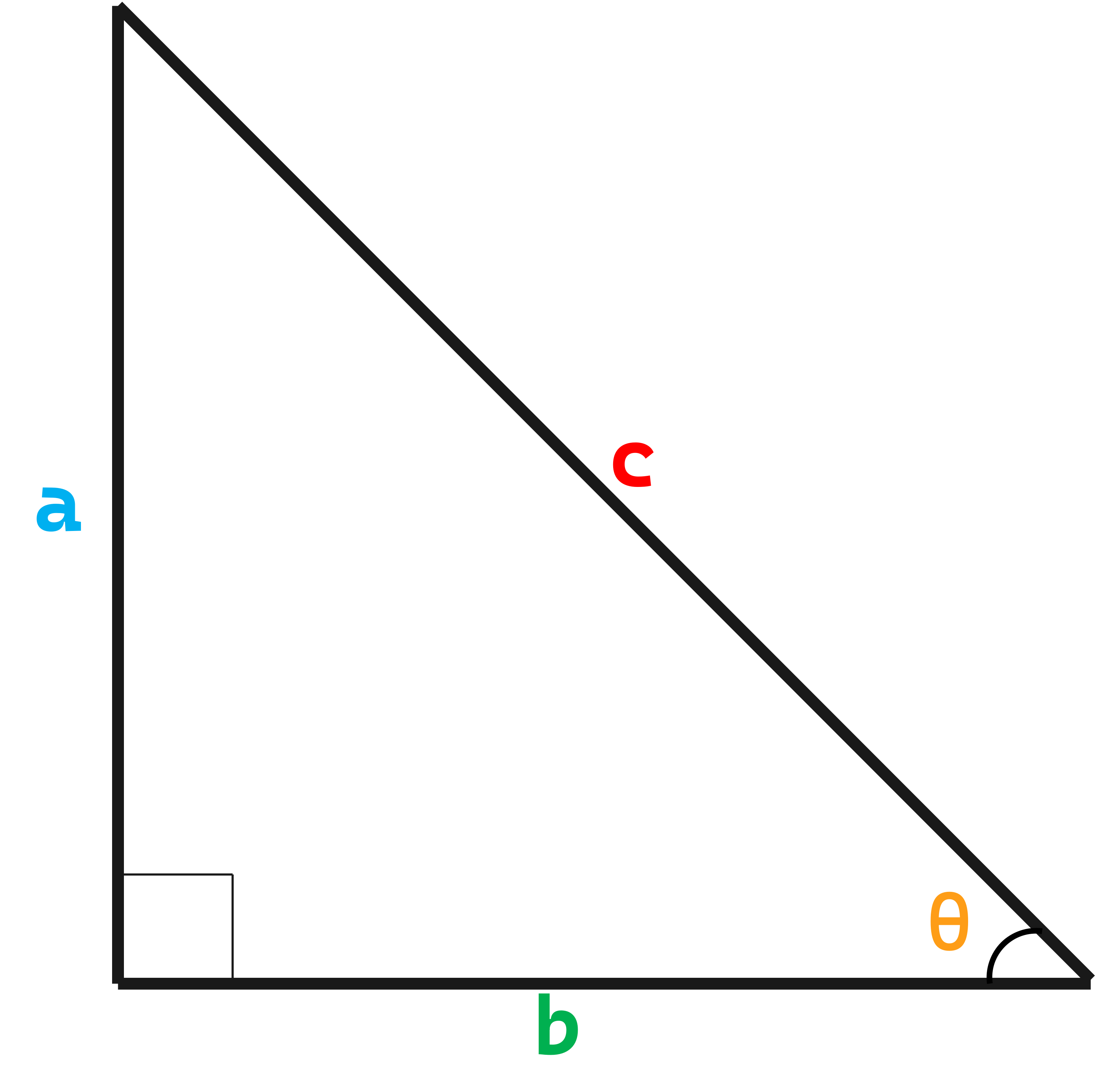
Find the value of csc²(y) using Pythagorean theorem:

$$ a = 1 $$

$$ b = x $$

$$ c^2 = ? $$

We need to solve for the value csc²(y) using the formula of Pythagorean theorem 

$$a^2 + b^2 = c^2 $$

$$(1)^2 + (x)^2 = c^2 $$

$$1 + x^2 = c^2 $$

Distribute the values to solve for csc²(y), we don't need to solve for c since c² = csc²(y)

$$ csc^2\medspace (y)=  1 + x^2 $$

Distribute the computed value of csc(y) from the previous equation:

$$ \dfrac{dy}{dx} = -\dfrac{1}{csc^2(y))} \enspace\enspace \enspace\longrightarrow\enspace\enspace   \dfrac{dy}{dx} = -\dfrac{1}{1+x^2}$$

The derivative of arccot(x) is:

$$\dfrac{d}{dx}(arccot(x)) = - \dfrac{1}{1+x^2}$$   

Practicing differential calculus problems will help us to further improve our mathematical skills. Don't hesitate to seek further resources such as textbooks , online courses, or interactive tutorials, to enhance your knowledge and refine your skills.

If you have any concern or inquiries, you can contact us through contact form or email us at: projectnullblogspot@gmail.com or you can leave a comment below.