Derivative of Inverse Trigonometric Functions arcsec(x) using Implicit Differentiation

In this another comprehensive tutorial, we will solve another problem related to differential calculus. This comprehensive guide offers a structured approach to effectively solving derivatives of an inverse trigonometric functions using the method of implicit differentiation.  Let's dive in and embark on this enriching adventure together, as we uncover the secrets of inverse trigonometric derivatives with invaluable mathematical knowledge.

$$ arcsec (x)$$

Let us complete the problem by equating  arcsec(x) in order to calculate and manipulate the problem easily:

$$ y = arcsec(x)$$

Isolate x by taking the secant of both sides:

$$ {\color{#FF0000} sec}  y =  {\color{#FF0000} sec} (arcsec(x))$$

Cancel the arc secant with secant as the two trigonometric functions are opposite, resulting to x:

$$sec(y) = \bcancel{sec} (\bcancel{arcsec}(x)) $$

 $$ sec(y) = x$$

Using implicit differentiation, find the derivative of both sec (y) using chain rule and x using power rule:

$$\color{#0000FF}  sec(y)\medspace tan(y) \color{#000000} \cdot \color{#008000} \dfrac{dy}{dx}   \color{#000000} = 1$$

Isolate terms that has dy/dx:

$$\dfrac{\bcancel{sec(y)tan(y)}\dfrac{dy}{dx}}{\color{#FF0000} \bcancel{sec(y)tan(y)}}  =  \dfrac{1}{\color{#FF0000} sec(y)\medspace tan(y)}  $$

$$ \dfrac{dy}{dx} = \dfrac{1}{sec(y)\medspace tan(y))} $$

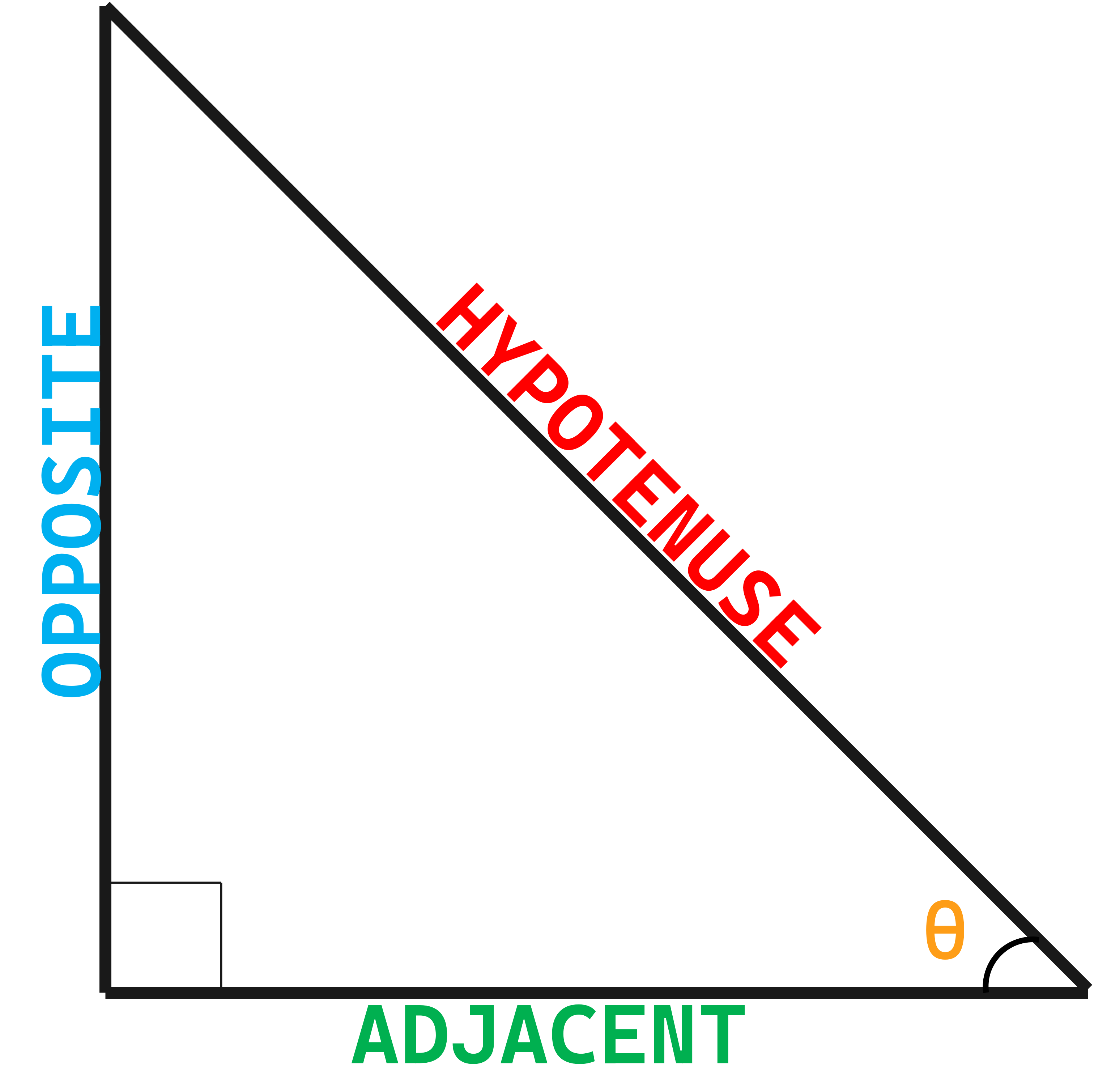
Find the values of sec(y) and tan(y) using Pythagorean theorem:

$$ sec\medspace \theta = \dfrac{\color{#FF0000} hyp}{\color{#008000} adj}\enspace\enspace \enspace\longrightarrow\enspace\enspace  sec\medspace (y) = \dfrac{\color{#FF0000} x}{\color{#008000} 1} $$

$$ tan\medspace \theta = \dfrac{\color{#0000FF} opp}{\color{#008000} adj}\enspace\enspace \enspace\longrightarrow\enspace\enspace  tan\medspace (y) = ? $$

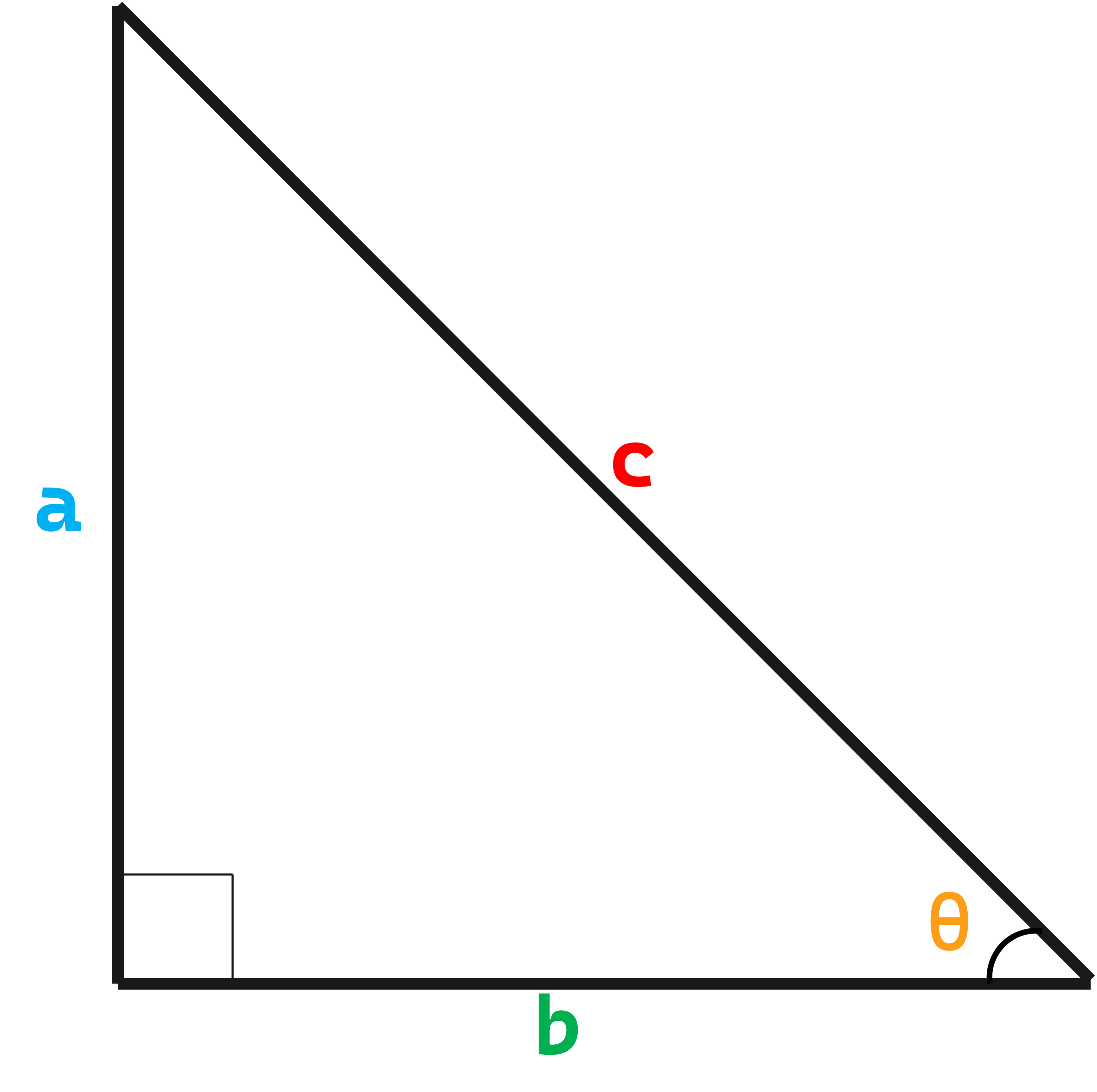
Let us solve and complete the sides of the right triangle in in order for us to solve tan(y):

$$a^2 + b^2 = c^2 $$

$$a^2 + (1)^2 = (x)^2 $$

$$a^2 + 1 = x^2 $$

$$a^2 = x^2 - 1 $$

$$\sqrt{a^2} = \sqrt{x^2 - 1}$$

$$a = \sqrt{x^2 - 1}$$

Distribute the values of the opposite and adjacent sides of the triangle to solve the equation of tan(y):

$$ tan\medspace (y)= \dfrac{\color{#0000FF} \sqrt{x^2 - 1}}{\color{#008000} 1} $$

$$ tan\medspace (y)=  \sqrt{x^2 - 1}$$

  

Distribute the computed values of sec(y) and tan(y) from the previous equation:

$$ \dfrac{dy}{dx} = \dfrac{1}{sec(y)\medspace tan(y))} \enspace\enspace \enspace\longrightarrow\enspace\enspace   \dfrac{dy}{dx} = \dfrac{1}{x\medspace\sqrt{x^2 - 1}}$$

The derivative of arcsec(x) is:

$$\dfrac{d}{dx}(arcsec(x)) = \dfrac{1}{x\medspace\sqrt{x^2 - 1}}$$   

In conclusion, understanding how to solve problems  related to derivatives of an inverse trigonometric function is a crucial skill to have specially when you are studying calculus. By mastering this, you can effectively tackle a wide range of problems in calculus, optimization, physics, engineering, and many other disciplines. Always remember that practice is the key to solidify your understanding of these concepts.

If you have any concern or inquiries, you can contact us through contact form or email us at: projectnullblogspot@gmail.com or you can leave a comment below.