Derivative of Inverse Trigonometric Functions arccot(x) using Implicit Differentiation

Welcome to our comprehensive tutorial on solving derivative of an inverse trigonometric function! If you've ever found yourself struggling with the intricacies of calculus or yearning to unlock the secrets of this mysterious functions, you've come to the right place. In this guide, we will take you on an enlightening journey through the world of inverse trigonometric derivatives, unraveling their complexities and providing with clear and intuitive understanding on how to conquer them.

$$ arccot (x)$$

Let us solve for arccot(x) by equating the problem with y:

$$ y = arccot(x)$$

Isolate x by taking the cotangent of both sides:

$$ {\color{#FF0000} cot}  y =  {\color{#FF0000} cot} (arccot(x))$$

Cancel the arc cotangent using its inverse function cotangent which will result to x, opposite functions in trigonometry undo the effect of each other:

$$cot(y) = \bcancel{cot} (\bcancel{arccot}(x)) $$

 $$ cot(y) = x$$

We can prove this by substituting 1 as x. If we first take the inside function arccos(1), we will have 0. and if we solve cos(0), it will return to the original value of x which is 1. 

Find the derivative of both cot(y) using chain rule and x using power rule:

$$\color{#0000FF}  -csc^2(y) \color{#000000} \cdot \color{#008000} \dfrac{dy}{dx}   \color{#000000} = 1$$

Isolate ^dy/_dx by multiplying both sides by ¹/_-csc²(y):

$$\dfrac{\bcancel{-csc^2(y)}\dfrac{dy}{dx}}{\color{#FF0000} \bcancel{-csc^2(y)}}  =  -\dfrac{1}{\color{#FF0000} csc^2(y)}  $$

$$ \dfrac{dy}{dx} = -\dfrac{1}{csc^2(y)} $$

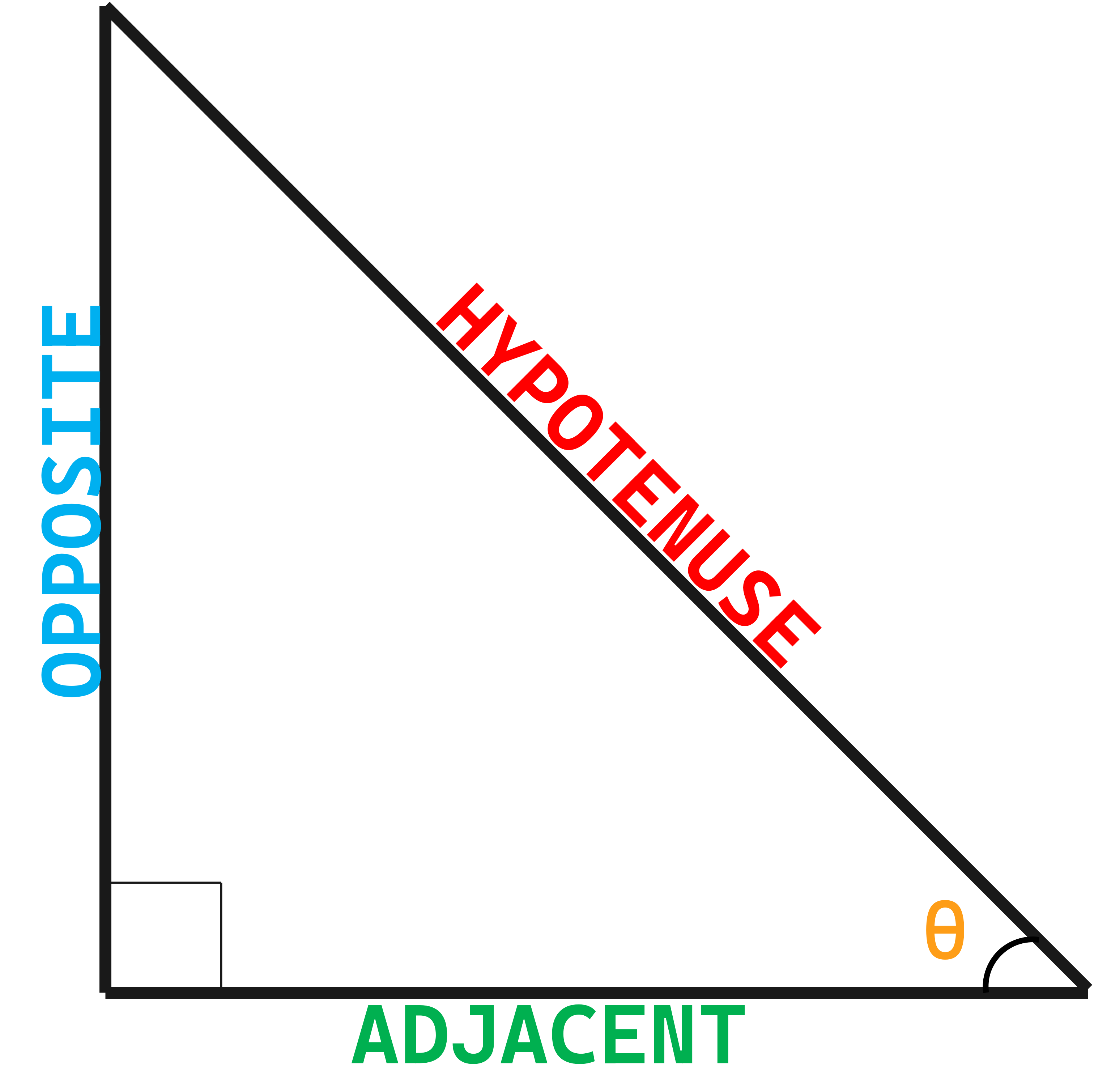
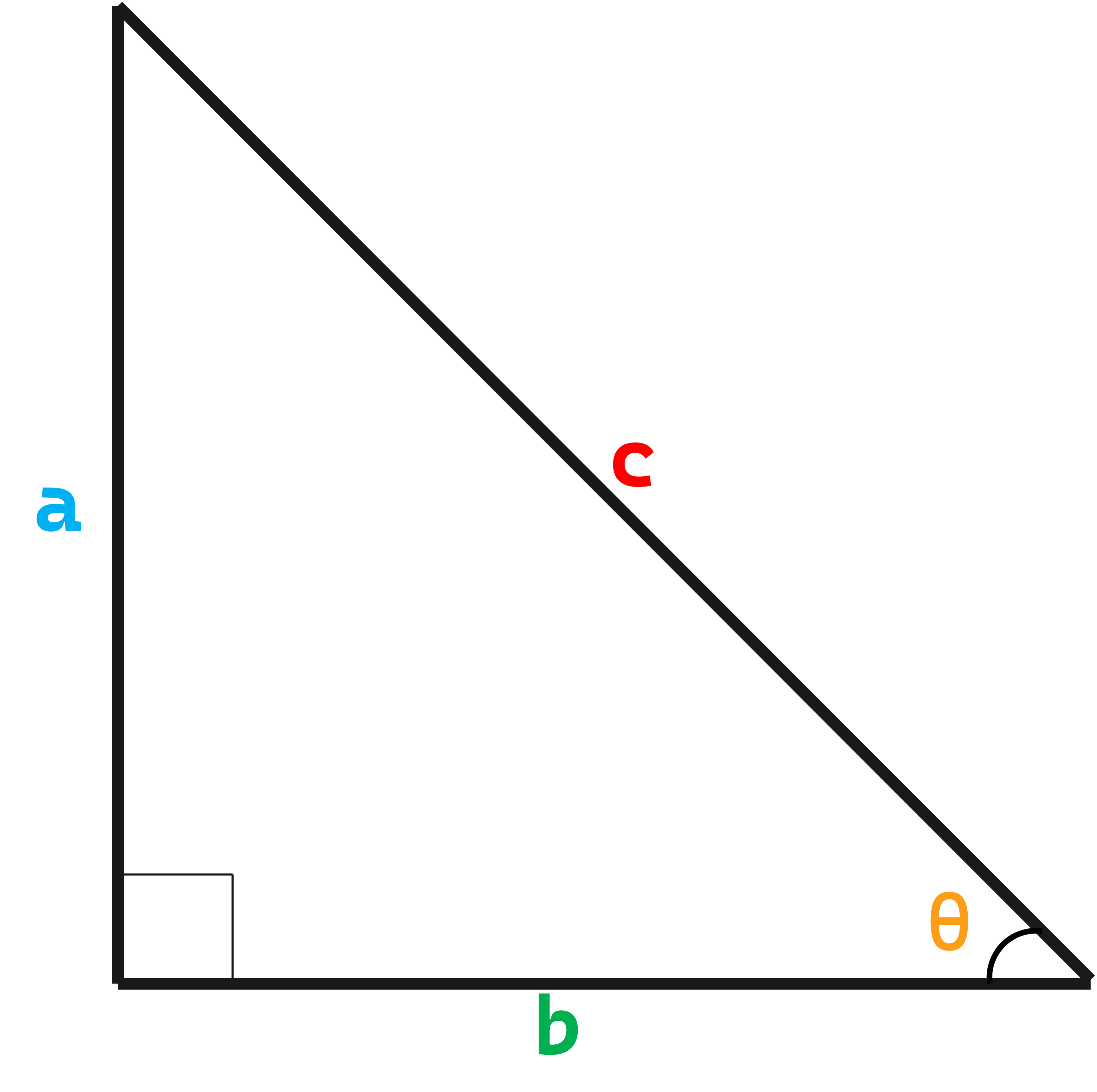
Find the value of csc²(y) using Pythagorean theorem:

$$ a = 1 $$

$$ b = x $$

$$ c^2 = ? $$

We need to solve for the value csc²(y) using the formula of Pythagorean theorem 

$$a^2 + b^2 = c^2 $$

$$(1)^2 + (x)^2 = c^2 $$

$$1 + x^2 = c^2 $$

Distribute the values to solve for csc²(y), we don't need to solve for c since c² = csc²(y)

$$ csc^2\medspace (y)=  1 + x^2 $$

Distribute the computed value of csc(y) from the previous equation:

$$ \dfrac{dy}{dx} = -\dfrac{1}{csc^2(y))} \enspace\enspace \enspace\longrightarrow\enspace\enspace   \dfrac{dy}{dx} = -\dfrac{1}{1+x^2}$$

The derivative of arccot(x) is:

$$\dfrac{d}{dx}(arccot(x)) = - \dfrac{1}{1+x^2}$$   

Practicing differential calculus problems will help us to further improve our mathematical skills. Don't hesitate to seek further resources such as textbooks , online courses, or interactive tutorials, to enhance your knowledge and refine your skills.

If you have any concern or inquiries, you can contact us through contact form or email us at: projectnullblogspot@gmail.com or you can leave a comment below.

Read More

Derivative of Inverse Trigonometric Functions arcsec(x) using Implicit Differentiation

In this another comprehensive tutorial, we will solve another problem related to differential calculus. This comprehensive guide offers a structured approach to effectively solving derivatives of an inverse trigonometric functions using the method of implicit differentiation.  Let's dive in and embark on this enriching adventure together, as we uncover the secrets of inverse trigonometric derivatives with invaluable mathematical knowledge.

$$ arcsec (x)$$

Let us complete the problem by equating  arcsec(x) in order to calculate and manipulate the problem easily:

$$ y = arcsec(x)$$

Isolate x by taking the secant of both sides:

$$ {\color{#FF0000} sec}  y =  {\color{#FF0000} sec} (arcsec(x))$$

Cancel the arc secant with secant as the two trigonometric functions are opposite, resulting to x:

$$sec(y) = \bcancel{sec} (\bcancel{arcsec}(x)) $$

 $$ sec(y) = x$$

Using implicit differentiation, find the derivative of both sec (y) using chain rule and x using power rule:

$$\color{#0000FF}  sec(y)\medspace tan(y) \color{#000000} \cdot \color{#008000} \dfrac{dy}{dx}   \color{#000000} = 1$$

Isolate terms that has dy/dx:

$$\dfrac{\bcancel{sec(y)tan(y)}\dfrac{dy}{dx}}{\color{#FF0000} \bcancel{sec(y)tan(y)}}  =  \dfrac{1}{\color{#FF0000} sec(y)\medspace tan(y)}  $$

$$ \dfrac{dy}{dx} = \dfrac{1}{sec(y)\medspace tan(y))} $$

Find the values of sec(y) and tan(y) using Pythagorean theorem:

$$ sec\medspace \theta = \dfrac{\color{#FF0000} hyp}{\color{#008000} adj}\enspace\enspace \enspace\longrightarrow\enspace\enspace  sec\medspace (y) = \dfrac{\color{#FF0000} x}{\color{#008000} 1} $$

$$ tan\medspace \theta = \dfrac{\color{#0000FF} opp}{\color{#008000} adj}\enspace\enspace \enspace\longrightarrow\enspace\enspace  tan\medspace (y) = ? $$

Let us solve and complete the sides of the right triangle in in order for us to solve tan(y):

$$a^2 + b^2 = c^2 $$

$$a^2 + (1)^2 = (x)^2 $$

$$a^2 + 1 = x^2 $$

$$a^2 = x^2 - 1 $$

$$\sqrt{a^2} = \sqrt{x^2 - 1}$$

$$a = \sqrt{x^2 - 1}$$

Distribute the values of the opposite and adjacent sides of the triangle to solve the equation of tan(y):

$$ tan\medspace (y)= \dfrac{\color{#0000FF} \sqrt{x^2 - 1}}{\color{#008000} 1} $$

$$ tan\medspace (y)=  \sqrt{x^2 - 1}$$

  

Distribute the computed values of sec(y) and tan(y) from the previous equation:

$$ \dfrac{dy}{dx} = \dfrac{1}{sec(y)\medspace tan(y))} \enspace\enspace \enspace\longrightarrow\enspace\enspace   \dfrac{dy}{dx} = \dfrac{1}{x\medspace\sqrt{x^2 - 1}}$$

The derivative of arcsec(x) is:

$$\dfrac{d}{dx}(arcsec(x)) = \dfrac{1}{x\medspace\sqrt{x^2 - 1}}$$   

In conclusion, understanding how to solve problems  related to derivatives of an inverse trigonometric function is a crucial skill to have specially when you are studying calculus. By mastering this, you can effectively tackle a wide range of problems in calculus, optimization, physics, engineering, and many other disciplines. Always remember that practice is the key to solidify your understanding of these concepts.

If you have any concern or inquiries, you can contact us through contact form or email us at: projectnullblogspot@gmail.com or you can leave a comment below.

Read More

Derivative of Inverse Trigonometric Functions arccsc(x) using Implicit Differentiation

In this tutorial, we will gain a deep understanding on solving problems related to differential calculus. This comprehensive guide offers a structured approach on effectively solving mathematical problems related to derivatives of an inverse trigonometric functions using the method of implicit differentiation. Implicit differentiation is an effective technique to solve for an inverse trigonometric function as we take the derivative of both sides with respect to x.   Let's immerse ourselves in the world of numbers and dominate the wonders of mathematics.

$$ arccsc (x)$$

Let us complete the problem by equating arccsc(x) to y in order to calculate and manipulate the problem as  y is dependent to the value of x and we can easily graph the equation:

$$ y = arccsc(x)$$

Isolate x by taking the cosecant of both sides:

$$ {\color{#FF0000} csc}  y =  {\color{#FF0000} csc} (arccsc(x))$$

Cancel arc cosecant with cosecant as the two trigonometric functions are opposite, resulting to x:

$$csc (y) = \bcancel{csc} (\bcancel{arccsc}(x)) $$

 $$ csc (y) = x$$

Using implicit differentiation, find the derivative of both csc y using chain rule and x using power rule with respect to x:

$$\color{#0000FF} - csc(y)\medspace cot(y) \color{#000000} \cdot \color{#008000} \dfrac{dy}{dx}   \color{#000000} = 1$$

Isolate terms that has dy/dx:

$$\dfrac{\bcancel{-csc(y)cot(y)}\dfrac{dy}{dx}}{\color{#FF0000} \bcancel{-csc(y)cot(y)}}  = - \dfrac{1}{\color{#FF0000} csc(y)\medspace cot(y)}  $$

$$ \dfrac{dy}{dx} = -\dfrac{1}{csc(y)\medspace cot(y))} $$

Find the values of csc(y) and cot(y) using Pythagorean theorem:

$$ csc\medspace \theta = \dfrac{\color{#FF0000} hyp}{\color{#0000FF} opp}\enspace\enspace \enspace\longrightarrow\enspace\enspace  csc\medspace (y) = \dfrac{\color{#FF0000} x}{\color{#0000FF} 1} $$

$$ cot\medspace \theta = \dfrac{\color{#008000} adj}{\color{#0000FF} opp}\enspace\enspace \enspace\longrightarrow\enspace\enspace  cot\medspace (y) = ? $$

Let's us solve and complete the sides of the right triangle in order for us to solve cot(y):

$$a^2 + b^2 = c^2 $$

$$(1)^2 + b^2  = (x)^2 $$

$$1 + b^2  = x^2 $$

$$b^2  = x^2 - 1 $$

$$\sqrt{b^2} = \sqrt{x^2 - 1}$$

$$b = \sqrt{x^2 - 1}$$

Distribute the values of the adjacent and opposite sides of the triangle to calculate for the value of cot(y):

$$ cot\medspace (y)= \dfrac{\color{#008000} \sqrt{x^2 - 1}}{\color{#0000FF} 1} $$

$$ cot\medspace (y)= \sqrt{x^2 - 1}$$

Distribute the computed values of csc(y) and cot(y) from the previous equation:

$$ \dfrac{dy}{dx} = -\dfrac{1}{csc(y)\medspace cot(y))} \enspace\enspace \enspace\longrightarrow\enspace\enspace   \dfrac{dy}{dx} = -\dfrac{1}{x\cdot\sqrt{x^2 - 1}}$$

The derivative of arccsc(x) is:

$$\dfrac{d}{dx}(arccsc(x)) = -\dfrac{1}{x\medspace\sqrt{x^2 - 1}}$$   

Practicing and understanding how to solve derivatives of an inverse trigonometric functions will help us further improve our mathematical skills. It is a valuable skill for anyone studying calculus or pursuing fields that involves advanced mathematics. 

If you have any concern or inquiries, you can contact us through contact form or email us at projectnullblogspot@gmail.com or you can leave a comment below.

Read More